Page 52 - فيزياء الصف الثالث الثانوي 1

يوناثلا ثلاثلا فصلا لولأا لصفلا ةيبرهكلا :ىلولأا ةدحولا - ءايزيف لا

لئاسملا لحل تاداشرإ

يلاوتلا ىلع تامواقم ةدع ليصوت ةلاح يف 1 -

R
R = R + R + R . ( ) ةئفاكملا ةمواقملا أ -
eq 1 2 3 eq

R = eq n R .n اهددعو R اهنم لك هميقو ةلثامتم تناك اذإ
=
I I = I = I 3 . (I) رايتلا ةدش سفن تامواقملا عيمجب رمي ب -
2
1
. V = V + V + V 3 تامواقملا نيب بسنلا سفنب تامواقملا ربع (V) ىلكلا دهجلا قرف عزوتي ج -
1
2
t
R R R
V = V  1 V = V  2 V = V  3
1
R + 1 R + 2 R 3 2 t R + 1 R + 2 R 3 3 t R + 1 R + 2 R 3
t

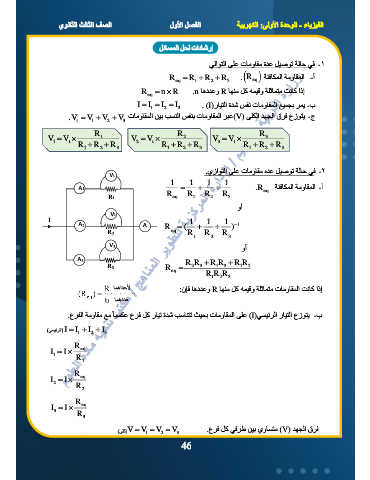
. يزاوتلا ىلع تامواقم هدع ليصوت ةلاح يف 2 -
1 V
1 1 1 1
1 A R = R + R + R . R eq ةئفاكملا ةمواقملا أ -

1 R eq 1 2 3
وأ
2 V
I 1 1 1
−
1
2 A A R = ( + + )
2 R eq R 1 R 2 R 3
3 V وأ

3 A R R + R R + R R
3 R R = 2 3 1 3 1 2
eq
R R R
1 2 3
امهادحلأ :نإف اهددعو R اهنم لك هميقو ةلثامتم تامواقملا تناك اذإ

امهددع

. عرفلا ةمواقم عم ًايسكع عرف لك رايت ةدش بسانتت ثيحب تامواقملا ىلع (I) يسيئرلا رايتلا عزوتي ب -
=
)يسيئرلا ( I I + I + I 3
2
1
R
I = I  eq
1
R
1
R
I = I eq
2
R 2

R
I = I  eq
3
R
3
=
V V = V = V . عرف لك يفرط نيب يواستم (V) دهجلا قرف
)ىلك ( 1 2 3
46